Curso
de Introducción al conocimiento científico experimental*
por Dra. Celia E. Coto
Capítulo 11. Visualización de los resultados
experimentales

Qué y cómo graficar.
Cuando se
realizan trabajos de investigación siempre se trata de expresar los resultados
en números porque la expresión cuantitativa permite un análisis objetivo que apoye
o rechace la hipótesis de trabajo.
Inicialmente, los valores
obtenidos son compilados en tablas o bases de datos, pero luego, y siempre que sea posible, conviene
convertirlos en una forma de representación
gráfica porque resulta difícil interpretar las relaciones existentes
entre los datos compilados en una tabla o cuadro. Los gráficos, por el
contrario, permiten una interpretación rápida de los resultados.
Independientemente del tipo exacto de gráfico, la creación de una visualización
clara y comprensible de datos tiene una importancia fundamental en todas las
ramas de la ciencia. De la misma manera, la lectura e interpretación de
gráficos es una habilidad primordial a todos los niveles, desde el estudiante
que recién se inicia al científico
experimentado. Los gráficos son componentes fundamentales de los trabajos de publicación
científicos, en los que los nuevos datos se presentan rutinariamente. A pesar
de que las tablas son necesarias para anotar datos, los gráficos le permiten al
lector visualizar complejas series de datos de una manera simple y concisa.
La forma de una curva, por
ejemplo, nos dice en forma inmediata si hay una relación directa entre las
variables, una tendencia hacia adónde evolucionarán los datos aún cuando no se
haya cubierto todo el espectro. Además las curvas permiten comparar entre
experimentos similares. De todos modos a medida que se experimenta se va
adquiriendo la habilidad necesaria para elegir cuál es la mejor forma de
representación. Son importantes los criterios de selección de una forma gráfica
que permita una lectura con claridad y facilite la comparación.
En la expresión escrita o en la
exposición oral de un trabajo científico se alternan gráficos, tablas,
esquemas, dibujos, gráficos generados por computadora y/o
fotografías obtenidas con el microscopio de luz, electrónico o por toma
directa.
En la actualidad la
representación gráfica se ha simplificado por el uso de software que permite la producción de las diferentes formas en que
se pueden agrupar los datos: tortas, barras o columnas, líneas y otras. Pero el
programa debe responder al criterio del investigador que decidirá cuál es la
forma correcta y más simple de graficar para poder interpretar los resultados.
No vamos a realizar un estudio exhaustivo del tema, sino que, mediante algunos
ejemplos pretendemos orientar a los lectores de este curso a desarrollar
criterios para seleccionar los modos más apropiados para expresar resultados
experimentales. Para la representación de los gráficos hemos utilizado el programa
de Microsoft Excel para MacOs 9.1.
Gráfico en forma de torta
Se trata de
un gráfico circular que provee un concepto visual de un todo, de modo que el
100% es igual a 360 grados. La torta se divide en segmentos, cada uno de ellos corresponde
a la categoría o clase de la variable representada. El tamaño de los segmentos
es proporcional al porcentaje de la categoría correspondiente. En una torta se
pueden agrupar datos de categorías específicas (conocidas también como
variables cualitativas) que pueden ser variables ordinales
o variables
nominales. Ejemplo: una variable ordinal
puede ser la altura porque refiriéndose a una persona puede ser alto, mediano o
bajo que guardan entre sí un orden aunque las distancias entre los valores no estén
definidas. La variable nominal describe un nombre, rótulo o clase entre las que
no hay un orden natural en consecuencia se pueden colocar en cualquier orden.
Ejemplo
1.
Se dispone de un alimento húmedo que se analiza para conocer
la concentración y composición relativa % de sus componentes. Los datos se
calcularon analizando 200g de alimento. Resulta claro que el tipo de variable
representada es nominal.
Cuadro 1. Composición nutricional de un alimento húmedo.
|
Clase |
Peso en gr |
% |
|
carbohidratos |
88 |
44 |
|
proteínas |
54 |
27 |
|
grasa |
22 |
11 |
|
agua |
36 |
18 |
Los datos de las columnas 1 y 3 señalados con sombra verde
los volcamos aun gráfico en forma de torta plana. (Figura 1).

Figura
1. Composición relativa por ciento de un alimento.
Se puede visualizar
rápidamente que casi la mitad del alimento está constituido por hidratos de
carbono.
La figura 2 muestra
lo mismo pero utilizando una torta tridimensional, a mi criterio esta representación
es más atractiva, pero es más fácil de interpretar la de la figura 1.

Figura
2. Composición relativa por ciento de un alimento
Es muy importante que los valores figuren al lado de cada porción y no
en el cuadro de referencias. Existen otro tipo de representaciones dentro del
grupo de las tortas en las que las porciones aparecen separadas como se ve en
la figura 3.

Figura
3.
Esta representación no ofrece ventajas respecto de las figuras 1 y 2
salvo en los casos en que se pueda graficar resaltando sólo una porción que se
quiere destacar. El programa usado no permitió esta representación pero existen
otros que sí lo permiten.
Ejemplo
2.
Cuando el número de variables es superior a 4 o 5 la representación en
forma de torta se vuelve más confusa, sobre todo si hay componentes en
proporción muy baja. La figura 4 es la representación gráfica de los datos del
cuadro 2.
Cuadro 2.
Composición nutricional de 100 gr de un alimento seco
Clase
|
Proporción porcentual (%) |
|
carbohidratos |
50 |
|
proteínas |
30 |
|
grasas |
2 |
|
fibra
alimenticia |
16 |
|
vitaminas |
1 |
|
minerales |
1 |

Figura
4. Representación gráfica de la composición porcentual del alimento.
La representación no es apta para visualizar las porciones más pequeñas
de la torta. Existen otro tipo de representaciones como las de forma de rosca
(doughnut) como se ve en

Figura
5. Representación porcentual de los datos del cuadro 2.
Nuevamente la proporción de los componentes
minoritarios no permite su visualización correcta en este caso la confusión es
mayor por la superposición de los datos de porcentaje. Para mejorar la
representación como se muestra en

Figura
6. Representación de los datos del cuadro 2.
Gráfico de barras.
Un gráfico de barras puede ser
horizontal o vertical pero lo más importante
es tener en cuenta la altura o longitud (horizontal) de la barra, cuanto
mayor es su altura o su longitud, mayor es el valor que representan.
Los gráficos de barras representan variables de categorías o
numéricas. Vamos a representar un gráfico de barras con los datos del cuadro 1,
vamos a obtener el gráfico de la figura 7.

Figura 7. Composición relativa por ciento de un alimento
(datos del cuadro 1)
Como podemos observar el gráfico de barras dimensiona los valores según
dos ejes, el vertical es la ordenada y el horizontal es la abscisa. Dicho de
otra forma: el vertical es el eje Y y el horizontal el eje X. La altura de las
barras se construyó con los valores de la columna 3 del cuadro 1. Aquí no es
necesario que las barras tengan colores distintos ya que se ve claramente la
diferente proporción de los componentes del alimento y su proporción está dada
por el valor que se lee sobre el eje de las X. La variable X es en este caso de
carácter nominal. En la figura 8 se muestra el mismo resultado pero las barras
aparecen en tres dimensiones.

Figura 8. Composición porcentual de un alimento (datos cuadro 1)
Estas columnas tridimensionales no le otorgan mayor claridad a la lectura
de los resultados.
Ejemplo
3.
Se dispone de un medicamento que elimina
manchas de la piel y se desea conocer si su efecto depende del sexo de la
persona (mujeres versus hombres) y se estudian los casos a las 24, 48 y 72
horas después de la aplicación. El
número de individuos voluntarios de cada muestra es idéntico. Si se asume que
los resultados obtenidos son los del cuadro 3 ¿cómo resultará la
representación?
Cuadro 3. Desaparición de las manchas en función del tiempo en hombres y
mujeres tratados.
|
grupo |
24 h |
48 h |
72 h |
|
mujeres |
30* |
40 |
60 |
|
hombres |
15 |
20 |
30 |
* expresado en %.
Los resultados se presentan en la figura 9, la variable X se
presenta en forma de intervalos correspondientes
a los días de lectura. El valor de Y es numérico.

Figura 9. Respuesta al tratamiento para quitar manchas de la
piel en hombre y mujeres.
El conjunto de números del eje Y
se denomina escala, en este caso el cero corresponde al punto de intersección
de ambos ejes. La escala tiene un valor máximo de 70 y los intervalos de la
escala valen 10 unidades.
Una lectura de este gráfico
muestra en forma inmediata que el medicamento fue más efectivo en las mujeres
que en los hombres y que no protege a todos los tratados siendo el máximo de
efectividad del 60% en las mujeres y el 30% entre los hombres, es decir, que
tiene una eficacia igual al doble entre las mujeres respecto de los hombres.
Además se puede deducir que su efecto aumenta con el tiempo que transcurre
desde su aplicación y además que por lo menos hay que esperar 72 horas para que
haya efecto. También podríamos sacar otras conclusiones. ¿Se animan?
Hay tres tipos de gráficos para representar datos de series
que dependen del tiempo, éstos son:
·
gráficos de barras
horizontales
·
gráficos de barras
verticales
·
gráficos de líneas
El gráfico 10 se construyó con los mismos datos salvo que
las barras son horizonatales y la figura 11 muestra los mismos resultados pero
con líneas.
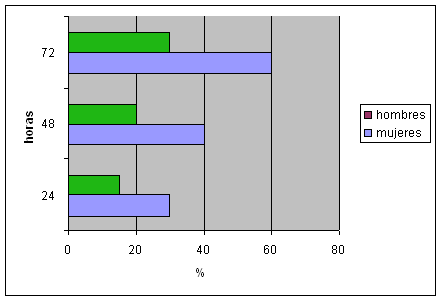
Figura 10.

Figura 11.
La conclusión sobre cuál es la forma más
rápida y mejor de representar los resultados se los dejo a ustedes lectores de
este capítulo.
Gráficos tipo curvas
Supongamos que realizamos un experimento con ratones en los que queremos
probar si la administración de tres drogas diferentes puede evitar la
mortalidad de los animales infectados con un virus. Para realizar el
experimento dividimos los ratones de igual peso y sexo en cuatro grupos (por
ejemplo de 10 animales cada grupo). El grupo control estará formado por ratones
infectados sin tratar. El grupo 1 con ratones infectados y tratados con la
droga 1, el grupo 2 de tratados serán infectados y tratados con la droga 2, el
grupo 3 ídem pero con la droga 3. Todos los días se observarán los animales y
se registrará el número de muertos en cada grupo por un período de 7 días al
cabo del cual se dará por terminado el experimento. Los resultados se volcaron
el en el cuadro 4.
Cuadro 4. Mortalidad de ratones infectados con un virus y tratados o no
con drogas.
|
Días post-infección |
Grupo control * |
Grupo tratado con droga 1 |
Grupo tratado con droga 2 |
Grupo tratado con droga 3 |
|
1 |
0 |
0 |
0 |
0 |
|
2 |
10 |
0 |
20 |
10 |
|
3 |
25 |
10 |
30 |
20 |
|
4 |
40 |
20 |
50 |
30 |
|
5 |
80 |
40 |
90 |
40 |
|
6 |
100 |
60 |
100 |
40 |
|
7 |
100 |
70 |
100 |
40 |
*
Los datos se expresan en mortalidad acumulada % es decir, a medida que
transcurren los días, se suman los números de muertos y se calcula el %. Los
valores oscilarán entre 0 y 100.
La
representación gráfica de estos resultados se ve en la figura 12.


Figura
12. Mortalidad comparada de grupos de ratones tratados o no.
Inmediatamente se deducen las siguientes conclusiones: la droga 2 es
tóxica, los animales mueren más rápido que los controles; la droga 1 protege al
20% de los animales como se ve al día 7 en que sobrevive el 20%. La droga 3 es
mejor aún ya que protege al 60% de los animales. Veamos qué pasa si se
representan estos datos en forma de barras, el gráfico corresponde a la figura
13.

Figura
13. Mortalidad comparada de grupos de ratones tratados o no.
Invitamos a nuestros lectores a sacar conclusiones
de las dos formas de representar. Finalmente nos vamos a referir a la elección
de la escala apropiada. Para esto nos servirá construir una curva de
crecimiento de un virus, tenemos que suponer que de alguna manera podemos
calcular el número de partículas virales que hay en el medio de cultivo. Cuando
un cultivo de células se infecta con un virus, las células son necesarias
porque los virus son parásitos, a medida que transcurren los días los virus se
van multiplicando hasta que al destruir todas las células del cultivo comienzan
a morir por efecto de la temperatura ya que son inestables a
Cuadro 5. Curva de crecimiento viral
|
Días post-infección |
Título de virus (número de partículas) |
|
1 |
---- |
|
2 |
100 |
|
3 |
1000 |
|
4 |
10.000 |
|
5 |
100.000 |
|
6 |
1.000.000 |

Figura
14. Curva de multiplicación viral
Los datos del cuadro 5 se volcaron en la curva de la figura 14. Como se
puede observar la escala del eje Y es una escala decimal y como los números son
tan grandes los datos de los primeros días quedan pegados ala eje de las X.
Esta representación es incorrecta, cuando se trabaja con números tan grandes la
escala de la ordenada debe ser logarítmica (figura 15), al realizar esta
transformación el gráfico se convierte inmediatamente en una recta que muestra
el crecimiento lineal del virus en función del tiempo de incubación.

Figura 15.
Curva de multiplicación viral
Conclusiones
Existen muchas otras posibilidades gráficas
para expresar los resultados de los experimentos provenientes del área de la química
o de la biología u otras ramas de las ciencias médicas. No las hemos analizado
todas el objetivo de este capítulo ha sido despertar el interés en la
graficación de los resultados que obviamente se pueden y deben tabular de modo
de lograr una mejor comprensión de lo que esos resultados nos indican.
Bibliografía:
Recomiendo un sitio de Internet de Canadá http://www.statcan.ca/start.html
donde encontrarán además de explicaciones para cada tipo de representación, un
glosario completo de términos necesarios relacionados con la estadística.
*Este
curso es una contribución de Química Viva educativa (e-Lab) a la propagación
del conocimiento científico entre los estudiantes de la escuela secundaria.
Departamento de Química Biológica. Facultad de Ciencias Exactas y Naturales.
Universidad de Buenos Aires.
Volver al menú de selección de capítulo.
|
|
Revista QuímicaViva Revista Electrónica del Depto. de Química Biológica, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina. quimicaviva@qb.fcen.uba.ar |